1. Introduction

In order to enhance the performance of traffic radar in traffic scenes, several methods have been developed, which can be roughly divided into two categories: (1) signal processing, aimed at minimizing or eliminating interference signals to ensure the clarity of target signals; (2) Improve the design of detection mechanisms.

The most direct way to suppress interference signals is to remove data samples affected by interference. However, this method not only eliminates interference, but may also affect the effective part of the target signal, thereby reducing the reconstruction accuracy of the useful signal. Therefore, an interference suppression technique based on the iterative matrix pencil (MP) method has been proposed, but its effectiveness is limited by the proportion of interfering samples. In order to further improve the accuracy of signal reconstruction, the method of sparse low rank decomposition of Hankel matrix is introduced, although this method increases the computational complexity. New solutions have emerged for the mutual interference between radars, such as developing novel orthogonal noise waveforms or utilizing techniques in the field of adjustable Q-factor wavelet transform (TQWT). In addition, some studies are exploring how to reduce signal distortion through transfer calibration of distance and Doppler units.

Improving the detection mechanism is another important way to enhance the effectiveness of radar applications. Although progress in this field is limited compared to interference suppression, it typically does not require additional hardware or computing resources, making it particularly suitable for low-cost radar systems equipped with lower performance processors. Considering that targets often appear in complex background noise and their characteristics change with time and spatial location, detection methods using fixed thresholds often cannot effectively distinguish targets from background noise. Therefore, radar constant false alarm rate (CFAR) detection technology has become an important tool for distinguishing targets from background noise by adjusting the detection threshold based on the current environment. A suitable CFAR algorithm can improve the detection efficiency of radar and ensure the accuracy of target information during radar data processing.

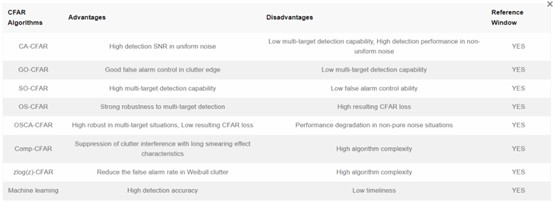
One of the earliest CFAR algorithms is Cell Average CFAR (CA-CFAR), which performs object detection by estimating the power level of local noise. It utilizes a reference window, where the central unit is considered a potential target, and the intensities of other units within the window are used to estimate background noise. In order to improve the poor detection performance of CA-CFAR in multi-target or non-uniform noise environments, maximum selection CFAR (GO-CFAR) and minimum selection CFAR (SO-CFAR) are proposed. GO-CFAR performs well in the boundary region, but there is a phenomenon of “target occlusion” in multi-target environments; SO-CFAR performs well in multi-target recognition, but its false alarm control is weak. Ordered Statistical CFAR (OS-CFAR) borrows the concept of median filtering, sorts samples in the reference window based on power values, and selects a specific sample as the decision threshold. Compared to CA-CFAR, OS-CFAR is more robust in multi-target detection, but may result in higher CFAR losses. To address these issues, new algorithms that combine OS and CA characteristics have emerged, such as Trimmed Mean CFAR (TM-CFAR).

With the increasing demand in different application scenarios, CFAR algorithms based on traditional methods have been developed. Some researchers focus on improving multi-target detection capabilities, such as the OSCA-CFAR algorithm that combines CA-CFAR and OS-CFAR. Some studies focus on improving detection performance in complex cluster environments, such as the Comp CFAR method based on the central limit theorem and signal logarithmic compression principle. In addition, some scholars have attempted to integrate machine learning techniques by training feedforward artificial neural networks (ANN) to improve CFAR detection efficiency, but this has also led to an increase in computational complexity.

Table 1 summarizes the various CFAR algorithms mentioned above. Although existing CFAR algorithms achieve object detection by designing a reference window and processing the data within it, the design of the reference window also has limitations. On the one hand, sliding windows may reduce detection efficiency, especially in LFMCW radar systems, where the two-dimensional sliding search of CFAR significantly affects the real-time performance of target detection due to the input being a two-dimensional distance Doppler matrix (RDM). On the other hand, the window size limits the number of samples available for background noise estimation, which may affect the accuracy of CFAR detection.

Fortunately, in road traffic scenes, background noise is relatively simple compared to complex backgrounds such as ocean surfaces. Especially in radar monitoring of moving targets, the use of zero Doppler technology can effectively eliminate the influence of background noise on the detection results. Considering the possible non ideal motion situations of vehicles during driving (such as turning, braking, lane changing), as well as the irregularity of target reflection areas and the independence of frame data, we assume that the echoes of moving targets on the road follow the ideal Swerling II model. Given this, in road traffic monitoring applications with relatively simple background noise, it may not be necessary to design a reference window for dealing with complex noise and interference. In fact, sliding windows actually increase the time complexity of the algorithm and reduce the efficiency of radar monitoring. In order to meet the low processing delay requirements of traffic monitoring radar systems, a CFAR algorithm based on Monte Carlo method is proposed to improve the detection efficiency and sensitivity of radar to moving targets in traffic environments. Compared with traditional methods, this algorithm not only improves detection sensitivity, but also eliminates the dependence on reference window design and sliding, thereby significantly reducing the time complexity of the algorithm and accelerating detection speed.

The main contributions of this study include: firstly, in the proposed CFAR detection algorithm, the entire range Doppler matrix (RDM) region is randomly sampled to obtain the sample points required for background noise power estimation. The core idea of this method is to apply the Monte Carlo simulation principle, which infers the characteristics of unknown variables through repeated independent experiments, to random sampling in RDM matrices. The advantage of doing so is that it breaks the limitation of the reference window and allows for the use of more sample points for background noise estimation. Secondly, by sorting and filtering the amplitude values of the sampling points, non background noise points (such as target points or interference points) are removed, thereby improving the accuracy of background noise estimation. Subsequently, the estimated power value of the background noise is obtained by taking the mean. Finally, the target points are extracted from the RDM matrix based on the background noise estimation results. In addition, the article also provides a method for setting algorithm parameters, which are obtained through multiple statistics based on the current physical platform and application environment. The parameter configuration process only needs to be executed once when the radar system environment is stable. Simulation and actual testing have shown that this method has significant advantages in detection sensitivity, detection accuracy, and detection delay compared to traditional methods, thereby improving the efficiency of radar detection in traffic monitoring.

2. Traffic scene

Usually, traffic sensors are installed on both sides of the road or on fixed brackets extending to the center of the road (as shown in Figure 1), and they need to have the following basic functions: high detection sensitivity. Capable of comprehensively detecting all targets in the field of view, even if the target is partially occluded, it can still be recognized· Low information latency performance. Being able to reflect traffic conditions in real time means that the time difference between data collection and road condition information output should be as short as possible (ideally, the delay should not exceed 100 milliseconds)· Weather resistance. Sensors should be able to minimize the impact of adverse weather conditions such as night time and fog on their performance.

Millimeter wave radar is considered an ideal choice for urban traffic monitoring due to its independence from environmental factors, high range resolution, and low application cost. As an important component of radar target extraction, CFAR detector has become a research focus. A new CFAR detection algorithm is proposed by analyzing the traditional CFAR algorithm and combining it with the specific characteristics of the traffic environment. The aim is to improve the sensitivity and multi-target detection ability of radar for target detection, while reducing time delay. It is hoped that this algorithm can provide unique insights for improving the applicability of radar in urban traffic monitoring.

3. Analysis of Radar Background Noise in Traffic Scenarios

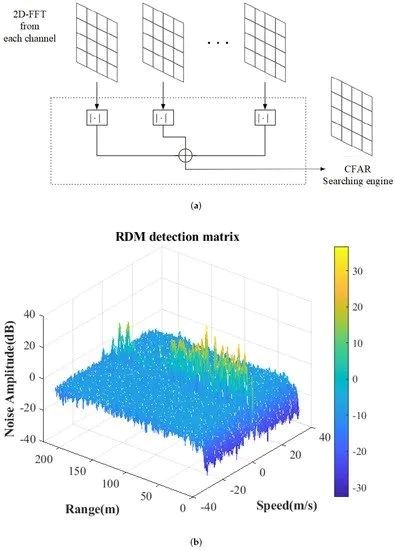
Figure 2 shows the process of collecting and displaying background noise data. Figure 2a provides a schematic diagram of the process for collecting continuous false positive detection data. In this radar system, four receiving channels are responsible for receiving radar electromagnetic echo signals from the background environment and generating a Range Doppler Matrix (RDM) through incoherent accumulation. Figure 2b shows the power amplitude distribution of RDM in the absence of moving targets. We can see that in the zero Doppler region (i.e. the region of stationary objects), the power amplitude exhibits a sudden and uneven distribution, which is due to the differences in the number of objects at different distances and the size of their reflection areas. Preliminary observations indicate that the noise power is evenly distributed in the non-zero Doppler region (i.e., the moving target area) without significant abrupt changes. In addition, the power distribution of stationary objects does not significantly extend to the area where the moving target is located.

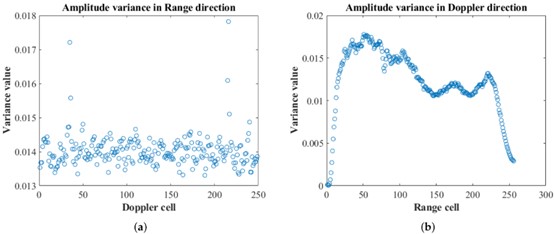
Using the variance of data in the distance and velocity dimensions as an effective measure of data dispersion to evaluate the distribution of noise power amplitude in the moving target area of the RDM matrix. This method calculates the variance of the dataset for each row (corresponding to the velocity dimension) or column (corresponding to the distance dimension) in RDM, as shown in Figure 3 (representing the average result of multiple statistical data). It is particularly important to note that before calculating the variance, pixels representing static objects with velocities below 0.5 meters per second in the RDM matrix were excluded based on the average pedestrian velocity (0.5 meters per second). The results show that the variances of the velocity and distance dimensions are both less than 0.018, indicating that the power amplitude distribution of background noise is relatively uniform in the non-zero Doppler region.

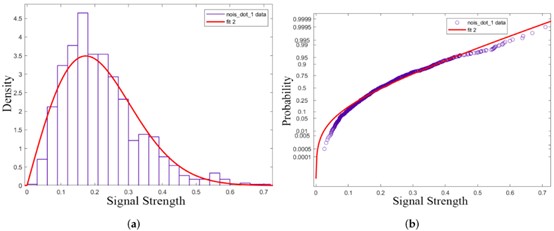
Power density distribution is another characteristic of background noise. Previously, it was assumed that the radar noise distribution follows a Rayleigh distribution:

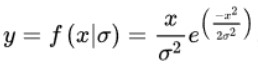
The non-zero Doppler cells in RDM were sampled and processed using the MATLAB distribution fitting toolbox, and the fitting curves of the data distribution (purple) and Rayleigh distribution (red) are shown in Figure 5a. Figure 5b shows the matching degree between the probability distribution of the data and the Rayleigh distribution, that is, the closer the data is to the curve, the greater its consistency with the Rayleigh distribution.